Abstract
It has been said that deriving the formulas for the ratios between the various gears of an epicyclic planetary gear system is non-intuitive and "taxes the human intellect" [1] To say the least. Internet searches for "How to" proved fruitless and dare I say information is being withheld, so this programmer set out to de-mystify the methods for calculating the widely used equations of motion for epicyclic planetary gear systems as referenced on the internet but never proven.

If you hate to see people getting rich by withholding knowledge then please help me. You can use this paper however you wish. You can re-distribute. You can archive on your servers, but please include the donation request. If you find this paper useful please consider a donation. Suggested donation is just $2 via PayPal to mrbuseco@buseco.net If you are an educator you are free to use it and distribute to students and donate as you think is fair. Please, anything will help. Thank you for considering. Sincerely, Matt W. Buse

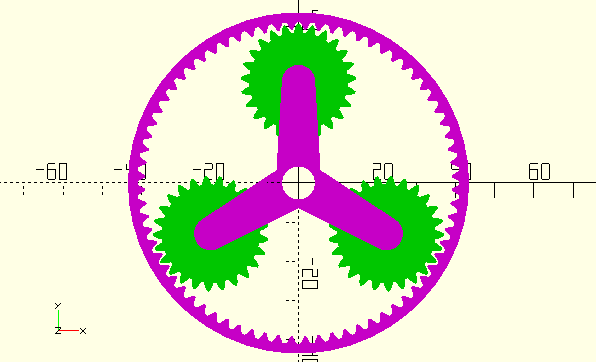
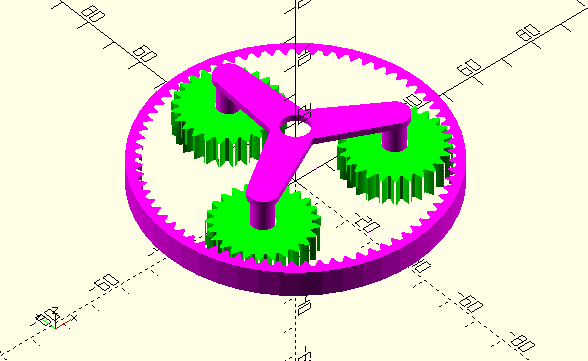
Figure 1. A typical epicyclic planetary gear system

By reason of the planet gears being connected to two other gears, carrier rotation is affected by two gear chains: (a) Sun-Planet-Carrier and (b) Ring-Planet-Carrier.

Figure 2. Sun-Planet-Carrier

---

Figure 3. Ring-Planet-Carrier

Analysis of Sun-Planet-Carrier Interaction

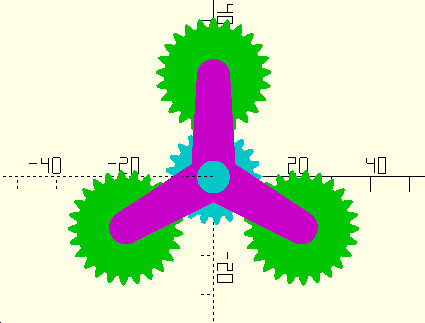We will first analyze Figure 2, the Sun-Planet-Carrier interaction. Let us remove the ring gear for the sake of clarity. Many "geared spinner" toys or 3D printable gearboxes are of such configuration and may be used to follow the mechanics described herein. Something the reader is encouraged to do as such activity led to this method of deriving the equations of motion.

First, we ask what happens if we just rotate the sun gear while the planets do not spin? If the planets do not spin then the system becomes a rigid body and the carrier would turn in unison by the same angle by which we turn the sun gear. We use the word "turn" for a gear to mean rotation about the central axis of that gear by some angle. It is completely analogous to angular velocity (ω) and can be used interchangeably therewith. Other variable definitions used throughout and herein are:

Turns of the Sun=Ts Turns of the Ring=Tr Turns of the Planet=Tp Turns of the Carrier=Tc

Number of teeth on sun = Ns Number of teeth on ring = Nr Number of teeth on planet = Np

If we rotate only the sun gear with planets locked we see simple rigid body rotation:

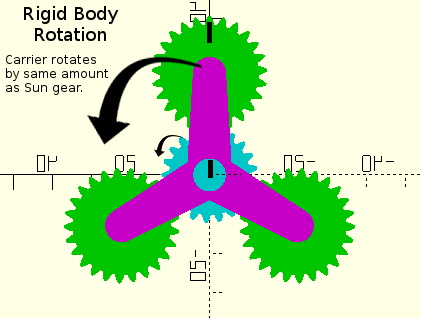Figure 4. Positions before rigid body rotation.

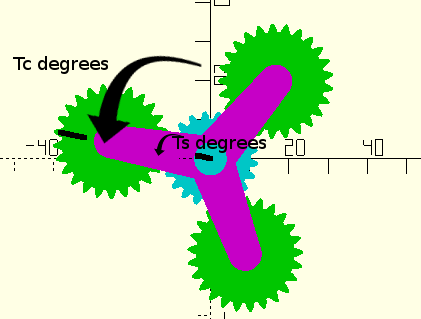Figure 5. Positions after rigid body rotation.

The indicator on the top gear shows we have not yet turned the planets.
As Ts is the rotation of the sun, and Tc is the rotation of the carrier then so far in the absence of the planets turning we have equal rotation of the sun and carrier. There will be another component added to the rotation due to planet rotation but at this point they are equal. Let us next rotate the planets and study the effect on the carrier.

From the position in Figure 5 we will now turn the planets while leaving the sun gear fixed. Since the planets are geared to the sun gear, this will cause them to in essence "crawl" over the sun gear bringing about additional rotation of the carrier.

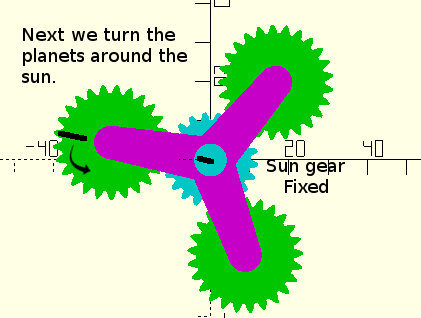Figure 6. Positions before turning planets

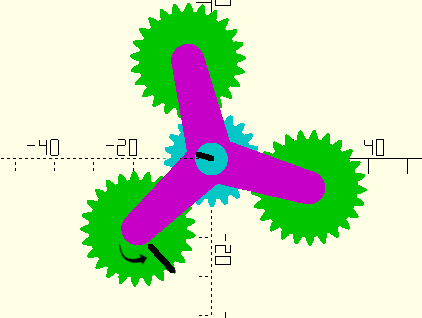Figure 7. Positions after turning planets

Notice by the center indicator that the sun gears stays fixed while the planets turn.
As we turned the planet gear it traversed the sun gear and imparted more rotation to the carrier. From our study of normal 2-gear interactions we know that the amount of traversal is determined by the number of teeth on each gear. We know that for each turn of the planet (Tp) the planet will travel around the sun (Np/Ns) times (taking the carrier with it in the process) where Np = Planet gear teeth and Ns = Sun gear teeth. The components are additive and carrier rotation is thus increased.

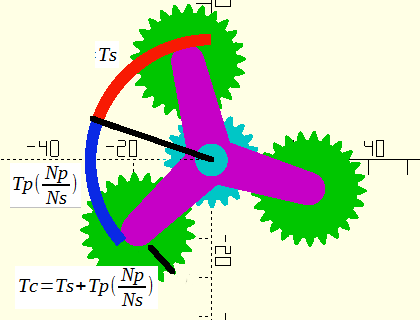Figure 8. Components of Carrier rotation attributable to Sun-Planet-Carrier interactions

The rotation of the carrier in the Sun-Planet-Carrier gear chain can now be described mathematically by the formula:

Formula 1

Analysis of Ring-Planet-Carrier Interaction

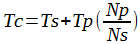Now we must determine the rotation relationship in the Ring-Planet-Carrier interaction. Let us add back the ring gear and remove the sun gear for clarity. As we did with the sun gear we will now turn the ring gear and not turn the planets. And again since the planets do not turn the apparatus becomes a rigid body and rotates in unison.

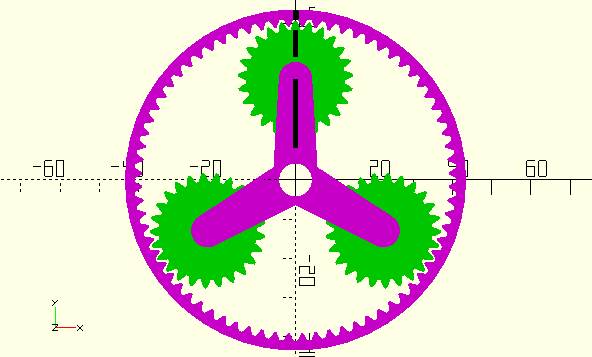Figure 9. Positions before rigid body rotation.

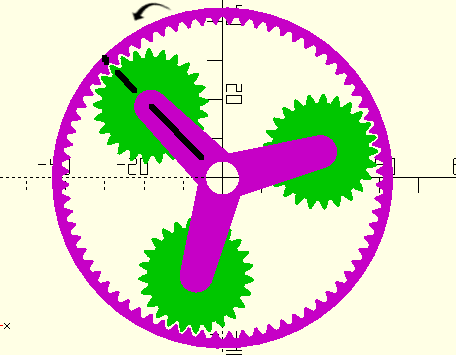Figure 10. Positions after rigid body rotation.

This is another case of rigid body rotation, this time by an amount Tr. Next we will turn the planets by a positive amount while keeping the ring gear fixed. Note the direction of travel of the carrier during positive turns of the planet gears. It is opposite the direction of Tr resulting in now a negative component to Tc.

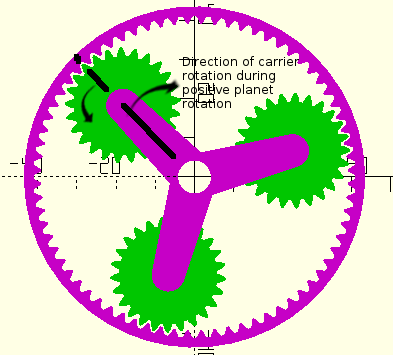Figure 11. Positions before turning planet.

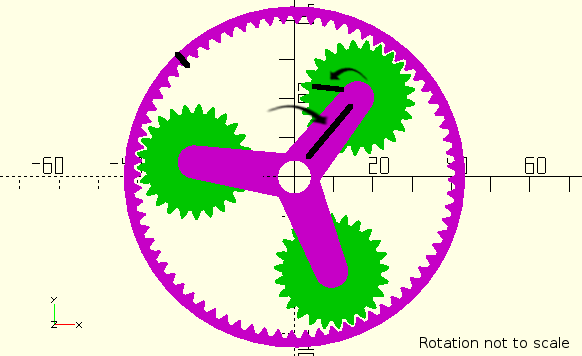Figure 12. Positions after turning planet.

Notice that the carrier turns by a negative amount during positive turns of the planet gears. We can think of the planet gear as "crawling" back in the opposite direction along the inside of the ring gear.

Now we are ready to add the components to obtain the net turn of the carrier based on the turns of the ring and planet gears:

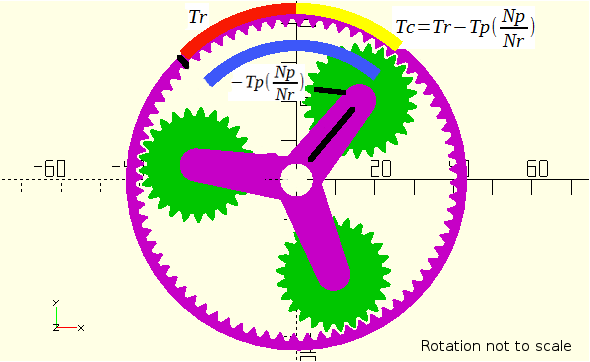Figure 13. Net effect (in yellow) of Ring and Planet turn on Carrier Rotation

From the motion visually displayed we can express Tc in the Ring-Planet-Carrier interaction by the formula:

Formula 2

---

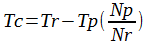We now have the two formulas:

In the complete apparatus, these relationships must hold true when both the sun and ring gears turn. Turning one must result in offsetting motion of the other to keep the equations in balance. They are inextricably linked and must hold true when connected together. We would like a final formula for describing the motion of the system in terms of the rotation of the sun (s), ring (r), and carrier (c) gears so we are not really interested in the turning of the planets (Tp). Also, by nature of the gear connections the motion of the planets is completely determined by the sun, ring, and carrier. While it would be possible to implant a motor to add torque, as long a sun and ring are present the planets cannot move independently of the gears they are attached to.

This being the case we will remove Tp from the equations:

(We start with our two equations)

Solving for Tp in the top and -Tp (to simplify cancellation) in the bottom leads to:



Now we add the two equations to eliminate Tp and obtain the following:



Multiplying both sides by Np removes the denominator and we re-arrange to get:

Formula 3

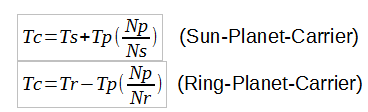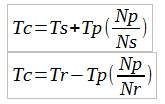
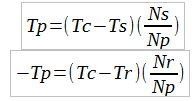
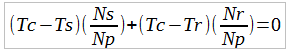
We re-arrange again:

Formula 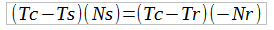4

(Multiply the right hand side by -1/-1 just so we can match some published equations)

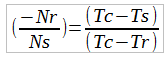
And finally we achieve the standard equations [2] for describing the relationship between ratios of turns in an epicyclic planetary gear system. We can use the above equations to generate derivative, yet equivalent equations of motion depending on our needs.

Example 1: How many turns must a sun gear turn to result in the carrier making one full rotation about it's axis if the ring gear is fixed and Nr=65 and Ns=26?

Solution: Using Formula 3 above and solving for Tc yields:


A fixed ring gear means Tr=0. If Nr=65 and Ns=26 then we get:


Taking the inverse tells us that it takes 3.5 turns of the sun gear to result in one complete turn of the carrier in the positive direction. (Note: These gear teeth ratios would not be used in practice.)

Matt Buse
mrbuseco@buseco.net

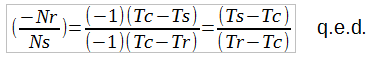
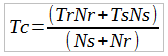
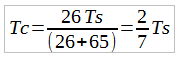
$2 Donation Appreciated

If you found this paper useful in learning about gears please consider making a small donation. Just $2 could make a huge difference and make much more such material available. PayPal ID: mrbuseco@buseco.net Text and images are available under the Creative Commons Attribution-ShareAlike License; additional terms may apply.

$2 Donation Appreciated